Choice of Preprocessing Methods: Scale, Standardize, Normalize
Many machine learning methods require the data to be approximately normally distributed and as close to that as possible. In Python, the popular package for machine learning is sklearn, which provides various functions for preprocessing including MinMaxScaler, RobustScaler, StandardScaler, and Normalizer. So, how should we choose among these methods? First, we introduce the differences, then we use actual data to observe the changes before and after processing, and finally, we provide a summary.
Definitions
- scale: Usually means changing the range of values while maintaining the shape of the distribution unchanged. Like scaling physical objects or models, this is why we say it changes proportionally. The range is usually set from 0 to 1.
- standardize: Standardization usually changes the values so that the standard deviation of the distribution equals 1.
- normalize: This term can be used for the above two processes, so to avoid confusion, it should be avoided.
Why?
Why do we perform standardization or normalization?
Because many algorithms run faster when handling standardized or normalized data. For example:
- Linear Regression
- KNN (K-Nearest Neighbors)
- Neural Networks (NN)
- Support Vector Machines (SVM)
- PCA (Principal Component Analysis)
- LDA (Linear Discriminant Analysis)
Generating Test Data
Data is generated using functions under np.random. Here, beta distribution, exponential distribution, normal distribution, and a normal distribution with different mean and scale are generated. The code is as follows:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# Set seed to ensure reproducibility
np.random.seed(1024)
data_beta = np.random.beta(1,2,1000)
data_exp = np.random.exponential(scale=2,size=1000)
data_nor = np.random.normal(loc=1,scale=2,size=1000)
data_bignor = np.random.normal(loc=2,scale=5,size=1000)
# Create dataframe
df = pd.DataFrame({"beta":data_beta,"exp":data_exp,"bignor":data_bignor,"nor":data_nor})
df.head()
# beta exp bignor nor
# 0 0.383949 1.115062 5.681630 3.384865
# 1 0.328885 0.831677 7.175799 3.036709
# 2 0.048446 8.407472 4.119069 -2.049115
# 3 0.108803 8.125079 10.164492 1.026024
# 4 0.376316 2.721583 6.848210 3.390942
View the distribution curves of this dataset:
sns.displot(df.melt(), x="value", hue="variable", kind="kde")
plt.savefig("origin.png", dpi=200)
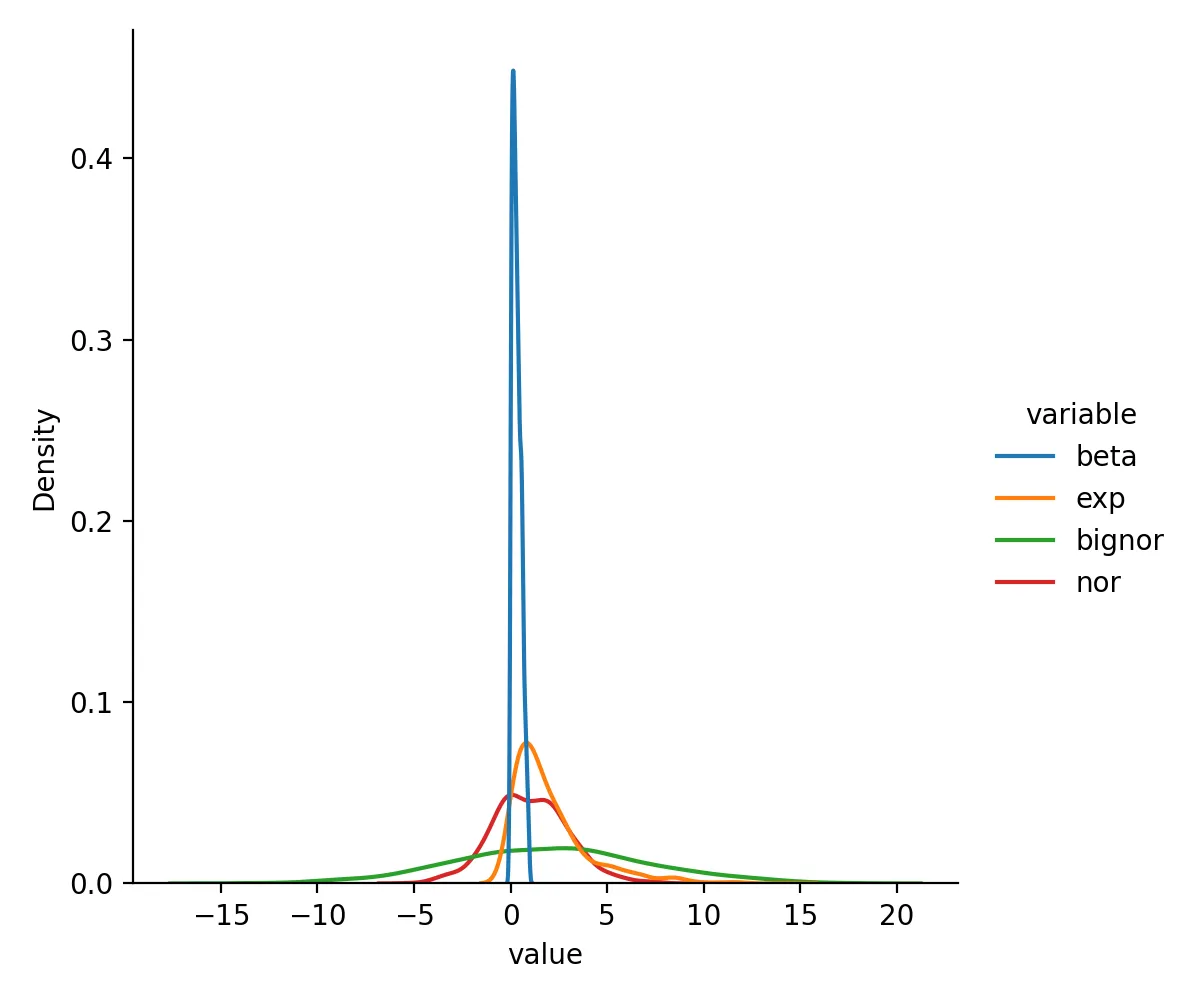
Comparing Data Changes After Different Processing
We apply MinMaxScaler, RobustScaler, and StandardScaler respectively and compare the results.
MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
df_minmax = pd.DataFrame(MinMaxScaler().fit(df).transform(df), columns=df.columns)
sns.displot(df_minmax.melt(), x="value", hue="variable", kind="kde")
plt.savefig("minmaxscaler.png", dpi=200)
plt.close()
Data after MinMaxScaler transformation looks like this:
beta exp bignor nor
0 0.402556 0.077887 0.623988 0.662302
1 0.344735 0.058066 0.671804 0.635879
2 0.050261 0.587947 0.573984 0.249901
3 0.113638 0.568196 0.767447 0.483282
4 0.394540 0.190253 0.661321 0.662763
Distribution is:
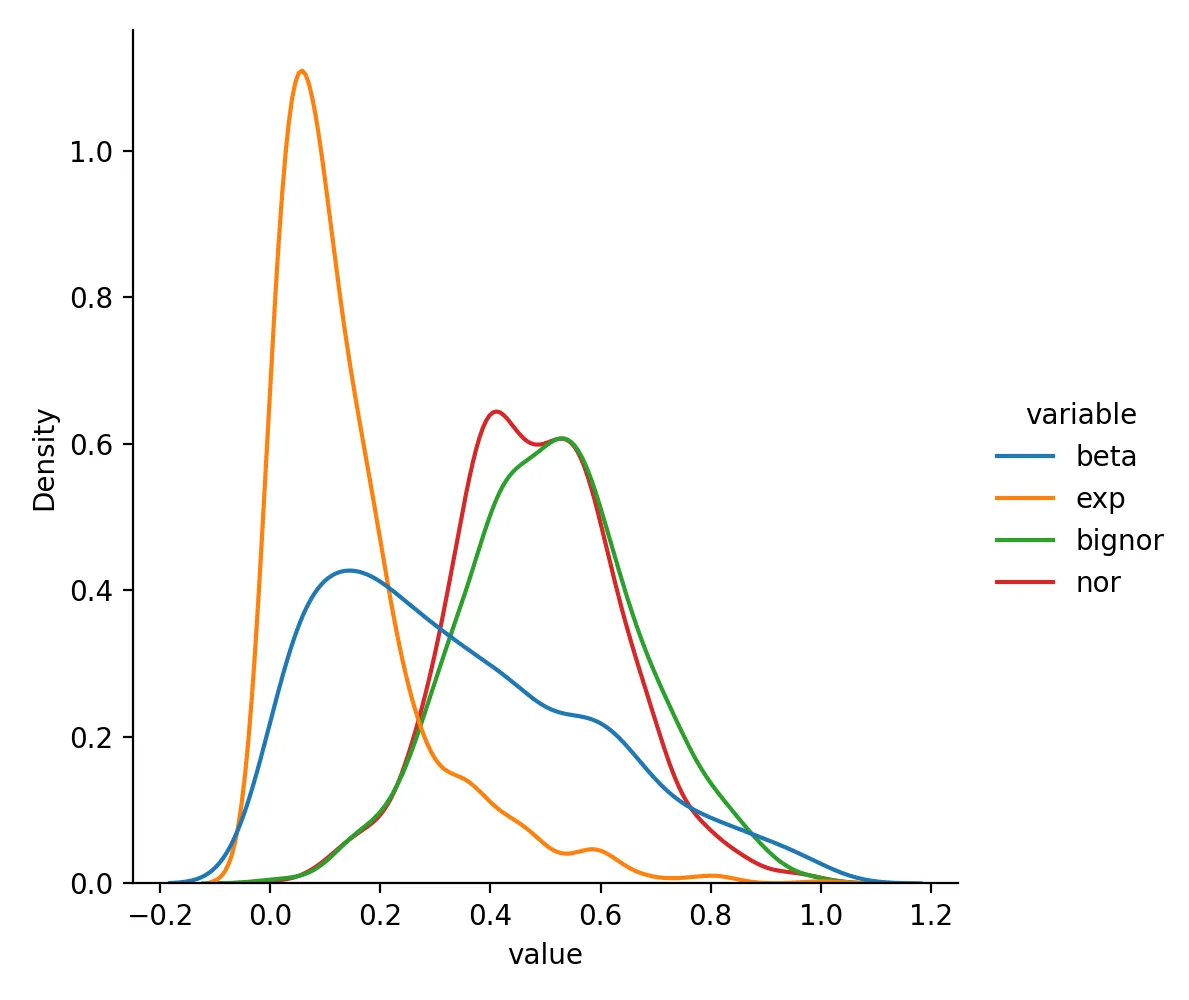
RobustScaler
from sklearn.preprocessing import RobustScaler
df_rsca = pd.DataFrame(RobustScaler().fit(df).transform(df), columns=df.columns)
sns.displot(df_rsca.melt(), x="value", hue="variable", kind="kde")
plt.savefig("robustscaler.png", dpi=200)
plt.close()
Data after RobustScaler transformation looks like this:
beta exp bignor nor
0 0.284395 -0.141315 0.551292 0.923234
1 0.126973 -0.278467 0.779068 0.790394
2 -0.674763 3.388036 0.313090 -1.150118
3 -0.502211 3.251365 1.234674 0.023211
4 0.262573 0.636202 0.729129 0.925553
Distribution is:
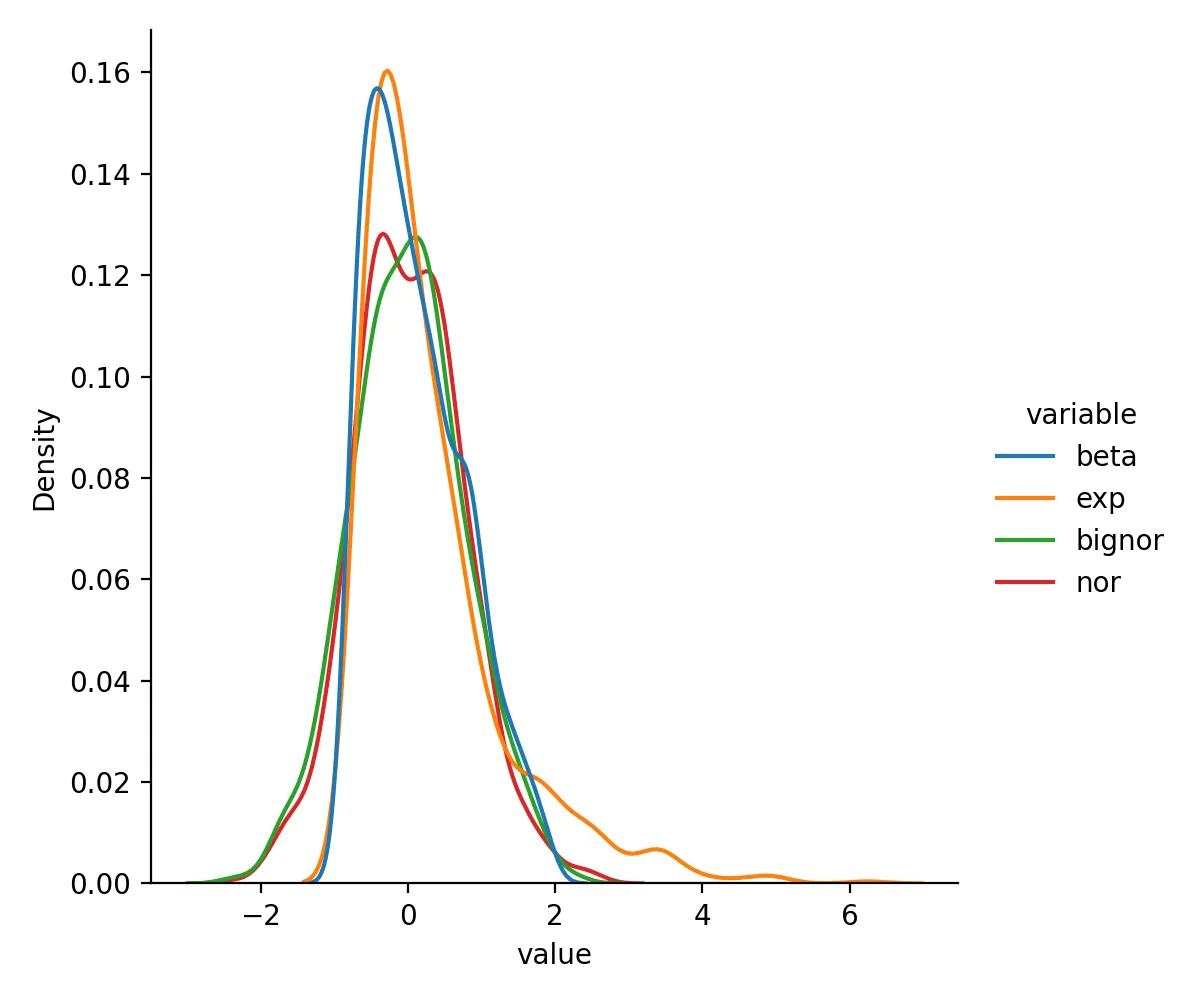
StandardScaler
from sklearn.preprocessing import StandardScaler
df_std = pd.DataFrame(StandardScaler().fit(df).transform(df), columns=df.columns)
sns.displot(df_std.melt(), x="value", hue="variable", kind="kde")
plt.savefig("standardscaler.png", dpi=200)
plt.close()
Data after StandardScaler transformation looks like this:
beta exp bignor nor
0 0.252859 -0.460413 0.711804 1.207845
1 0.012554 -0.600899 1.008364 1.030065
2 -1.211305 3.154733 0.401670 -1.566938
3 -0.947902 3.014740 1.601554 0.003337
4 0.219547 0.336005 0.943345 1.210949
Distribution is:
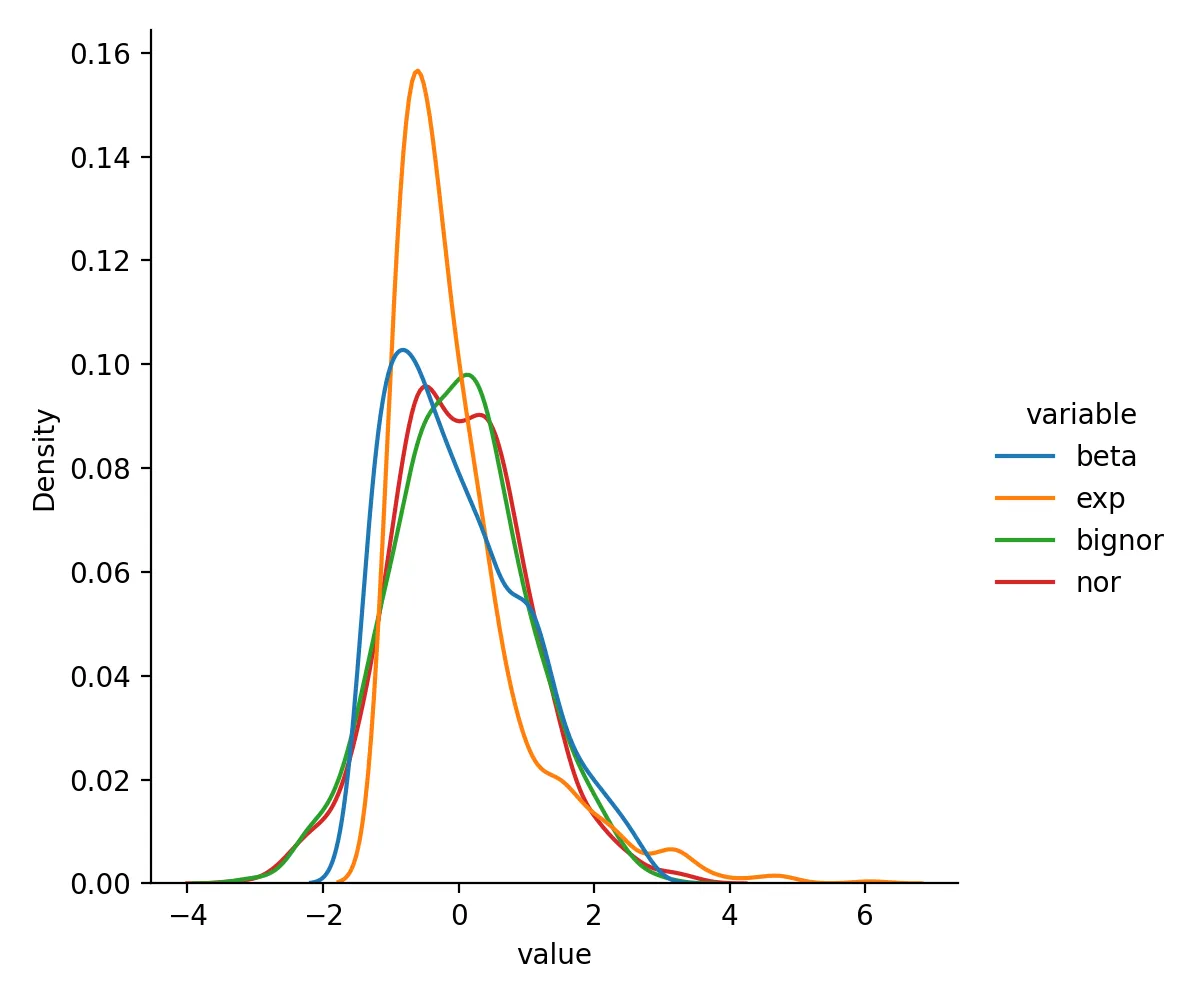
Summary
This article summarized various methods of standardization and normalization, the benefits of using these methods, and their effects on data distribution. Generally speaking, using standardization is the more common practice.
- 原文作者:春江暮客
- 原文链接:https://www.bobobk.com/en/981.html
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。