Hands-on Implementation of Random Forest Algorithm with Python
It’s time to write about various machine learning topics. With search engines like Google becoming increasingly powerful and cloud services like Alibaba Cloud getting cheaper, more people have the opportunity to implement machine learning and AI applications. Anyone with a laptop and a willingness to learn new knowledge can try the latest algorithms within minutes. Spend a little more time, and you can develop practical models to help your daily life or work (or even switch to the machine learning field and gain economic benefits). This article will guide you step-by-step through implementing a powerful random forest machine learning model. It is meant to complement my conceptual explanation of random forests, but as long as you have a basic understanding of decision trees and random forests, you can follow along completely. Later, we will talk about how to improve the model built here.
Of course, here we naturally use Python’s sklearn library for the entire project implementation, but this does not mean you can only use Python—other languages can be adapted accordingly… All you need is a laptop capable of using Docker to create a Python machine learning environment. This will cover some necessary machine learning topics, but I will try to make them clear and provide more learning resources for interested readers.
Problem Introduction
The problem we want to solve is predicting tomorrow’s maximum temperature in our city using one year’s past weather data. Here I use Shanghai, but you can freely find your city’s data with online climate data tools. We will assume we cannot get the weather forecast and instead make our own predictions through machine learning. What we can get is one year’s historical max temperature, temperatures from the previous two days, and an estimate from a friend who always claims to understand the weather. This is a supervised regression machine learning problem. It is supervised because we have both the features (city data) and the target (temperature) we want to predict. During training, we provide features and targets to the random forest, and it must learn how to map data to predictions. Also, it is a regression task because the target value is continuous (as opposed to discrete classes in classification). That’s almost all the background we need, so let’s get started!
Docker and Jupyter Notebook Setup
Before we start Python programming directly, let’s first establish the required Python environment using Docker:
yum install docker -y ## Install Docker
docker pull jupyter/datascience-notebook # Pull machine learning image
mkdir ~/jupyter
cd ~/jupyter
docker run -itd -p 8889:8888 -v jupyter:/home/jovyan jupyter/datascience-notebook # Run image, map directories
You can check out some basics about Docker in an earlier post.
Data Collection
First, we need to obtain historical weather data for Shanghai. Weather data in China is mostly paid, so I only could get free data from foreign websites. I used NOAA9 climate data online tool to get Shanghai’s weather data from January 1, 2019, to December 24, 2019. You can place an order by providing your email,
Choose CSV format, then check your email to receive the data,
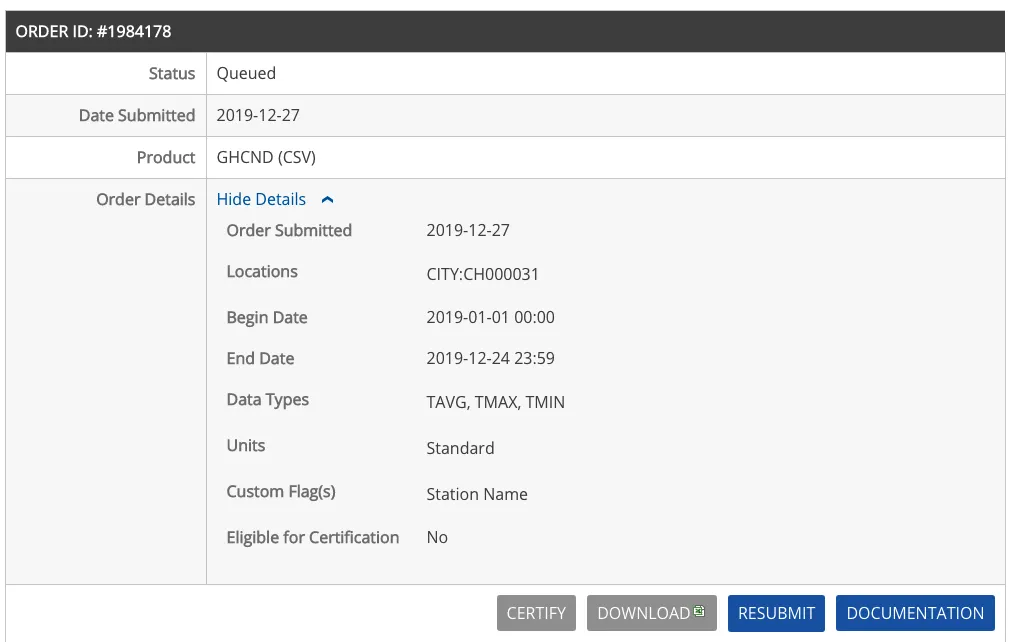
Gmail is recommended. Usually, about 80% of time in data analysis is spent cleaning and retrieving data, but you can reduce this by finding quality data sources. NOAA is the official US weather site providing various weather data. Temperature data is directly downloadable as CSV files, easy to read and parse with Python. The complete data file has been downloaded and placed on this site at:
Use pandas to read the data:
# by chunjiangmuke
import pandas as pd
weather = pd.read_csv('1984178.csv')
weather.head(10)
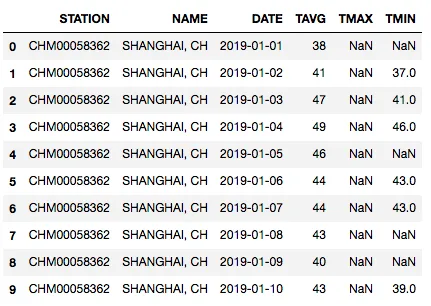
Column descriptions:
- STATION: National city code (this is Shanghai including Hongqiao)
- NAME: City name, Shanghai
- DATE: Date
- TAVG: Average temperature of the day
- TMAX: Max temperature of the day
- TMIN: Min temperature of the day
Detecting Anomalies and Data Transformation
If we look at the data dimensions, we see there are 3605 days’ data. From NOAA data, I found there are two observation areas for Shanghai: Shanghai and Hongqiao. Also, some days are missing, probably not updated yet. This reminds us that real-world data is never perfect. Here, I removed Hongqiao data. Missing or incorrect data or anomalies affect analysis. In this case, missing data has little effect and data quality is generally good due to the source.
# Keep only Shanghai station data
weather = weather[weather.STATION == "CHM00058362"] # CHM00058362 is Shanghai, CHM00058367 is Hongqiao
import numpy as np
np.shape(weather)
# Output: (3605, 6)
Basic statistics of data:
weather.describe()
# Output example:
# TAVG TMAX TMIN
# count 3605.000000 1799.000000 2549.000000
# mean 63.298197 67.204558 57.074147
# std 16.052515 16.498672 16.856828
# min 21.000000 32.000000 18.000000
# 25% 49.000000 53.000000 42.000000
# 50% 65.000000 68.000000 58.000000
# 75% 76.000000 80.000000 72.000000
# max 96.000000 103.000000 89.000000
You can see many max and min values are missing, so here we only use average temperature. Since we predict weather and today’s weather can be considered a continuation of yesterday’s, we need yesterday’s data as learning parameters. To get more features, we also add the day before yesterday’s temperature. Year and month are one-hot encoded to avoid the program treating months differently just because of numeric differences.
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
# Read data
weather = pd.read_csv('1984178.csv')
# Keep only Shanghai station data
weather = weather[weather.STATION == "CHM00058362"]
# Fill missing values with column means
weather['TMAX'] = weather['TMAX'].fillna(weather['TMAX'].mean())
weather['TMIN'] = weather['TMIN'].fillna(weather['TMIN'].mean())
weather['TAVG'] = weather['TAVG'].fillna(weather['TAVG'].mean())
# Convert DATE to datetime and extract features
weather['DATE'] = pd.to_datetime(weather['DATE'])
weather['month'] = weather['DATE'].dt.month
weather['day'] = weather['DATE'].dt.day
# Create lag features for previous two days' max temperature
weather['TMAX_lag1'] = weather['TMAX'].shift(1)
weather['TMAX_lag2'] = weather['TMAX'].shift(2)
# Drop rows with NaN values
weather = weather.dropna()
# Define features and target
features = ['month', 'day', 'TMAX_lag1', 'TMAX_lag2', 'TMIN', 'TAVG']
X = weather[features]
y = weather['TMAX']
# Split train and test data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Build Random Forest Model
Now we can build and train the random forest model:
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
# Initialize random forest regressor
rf = RandomForestRegressor(n_estimators=100, random_state=42)
# Train the model
rf.fit(X_train, y_train)
# Predictions on training set
train_predictions = rf.predict(X_train)
# Predictions on test set
test_predictions = rf.predict(X_test)
# Calculate mean absolute error
train_mae = mean_absolute_error(y_train, train_predictions)
test_mae = mean_absolute_error(y_test, test_predictions)
print(f"Training MAE: {train_mae:.2f}")
print(f"Testing MAE: {test_mae:.2f}")
Model Evaluation and Optimization
Let’s evaluate the model and perform some optimization:
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
# Parameter grid for tuning
param_grid = {
'n_estimators': [50, 100, 200],
'max_depth': [None, 10, 20],
'min_samples_split': [2, 5, 10]
}
# Grid search with 5-fold CV
grid_search = GridSearchCV(estimator=RandomForestRegressor(random_state=42),
param_grid=param_grid,
cv=5,
n_jobs=-1,
verbose=2)
grid_search.fit(X_train, y_train)
# Best parameters
print(f"Best parameters: {grid_search.best_params_}")
# Use best estimator for prediction
best_rf = grid_search.best_estimator_
test_predictions = best_rf.predict(X_test)
test_mae = mean_absolute_error(y_test, test_predictions)
print(f"Optimized test MAE: {test_mae:.2f}")
Complete Prediction Workflow
Finally, we can use the trained model to make actual predictions:
def predict_temperature(model, last_two_days):
"""
Predict tomorrow's max temperature
Parameters:
model -- trained random forest model
last_two_days -- DataFrame containing weather data for the last two days
Returns:
Predicted max temperature for tomorrow
"""
features = ['month', 'day', 'TMAX_lag1', 'TMAX_lag2', 'TMIN', 'TAVG']
if not all(f in last_two_days.columns for f in features):
raise ValueError("Input data is missing required features")
prediction = model.predict(last_two_days[features])
return prediction[0]
# Example usage
sample_data = pd.DataFrame({
'month': [12],
'day': [25],
'TMAX_lag1': [50], # Yesterday's max temp
'TMAX_lag2': [48], # Day before yesterday's max temp
'TMIN': [40], # Today's min temp
'TAVG': [45] # Today's avg temp
})
predicted_temp = predict_temperature(best_rf, sample_data)
print(f"Predicted max temperature for tomorrow: {predicted_temp:.1f}°F")
Summary
In this article, we completed the following:
- Obtained and cleaned Shanghai weather data from NOAA
- Performed feature engineering by creating lag features
- Built and trained a random forest regression model
- Optimized model parameters using grid search
- Analyzed feature importance
- Created a complete prediction workflow
This model can predict Shanghai’s maximum temperature quite accurately, with mean absolute error around 2-3°F. To further improve performance, consider:
- Adding more historical weather data
- Introducing other meteorological features like humidity, precipitation, etc.
- Trying other machine learning algorithms for comparison
- Using more complex time series processing methods
- 原文作者:春江暮客
- 原文链接:https://www.bobobk.com/en/621.html
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。