主成分分析背后的数学原理及python实例演示

本文将介绍机器学习中非常重要的降维的一种处理方法，主成分分析。

PCA介绍

在多元统计分析中，主成分分析（英语：Principal components analysis，PCA）是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分（PC）。具体地，主成分可以看做一个线性方程，其包含一系列线性系数来指示投影方向。PCA对原始数据的正则化或预处理敏感（相对缩放）。主成分分析的中心思想是在稀疏矩阵中，通过一些手段减少由大量相互关联的变量组成的数据集的维数，同时尽可能保留数据集中存在的变化。这是通过将一组不相关且有序的主变量（PC）转换为一组新变量来实现的，从而使前几个变量保留了所有原始变量中存在的大部分变化，从而达到较少数据维度的作用。

PCA背后的数学原理及python演示

接下来介绍pca后面的具体操作过程。PCA可以看作是无监督的学习问题。从原始数据集中获取主成分的整个过程可以分为六个部分：

将整个数据集包含d + 1维转化不含标签项的d维数据。
计算整个数据集每个维度的均值。
计算整个数据集的协方差矩阵。
计算特征向量和相应的特征值。
通过减少特征值对特征向量进行排序，并选择特征值最大的k个特征向量以形成d×k维矩阵W。
使用此d×k特征向量矩阵将样本转换到新的子空间上

下面一项一项说明

将整个数据集包含d + 1维转化不含标签项的d维数据

将整个数据集包含d + 1维，并剔除数据标签，也就是需要预测的结果y，以使我们的新数据集成为d维。假设我们有一个d + 1维的数据集。在现代机器学习范例中，可以将d视为X_train，将标签项视为y_train （标签）。因此，X_train + y_train构成了我们完整的训练数据集。因此，在删除标签y_train后，剩下的是d维数据集，这将是我们用来进行主成分分析的数据集。另外，假设忽略标签即d = 3之后，我们剩下一个三维数据集。我们将假设样本来自两个不同的类别，其中数据集的一半样本标记为1类，另一半标记为2类。假设我们的数据矩阵score为不同学生语数英三个学科的分数。category为学生类型该矩阵如下

import numpy as np
import pandas as pd

###学生分数矩阵
stu_score = stu_score = np.matrix([[90,60,80,0],[90,100,40,0],[80,90,70,0],[60,60,60,1],[70,60,50,1],[70,50,30,1]])
stu_score
##matrix([[ 90,  60,  80,   0],
#        [ 90, 100,  40,   0],
#        [ 80,  90,  70,   0],
#        [ 60,  60,  60,   1],
#        [ 70,  60,  50,   1],
#        [ 70,  50,  30,   1]])

###分数矩阵
score = stu_score[:,:3]
### 学生分类
category = stu_score[:,3]

计算整个数据集每个维度的平均值。

上表中的数据可以用矩阵A表示，矩阵中的每一列显示测试的具体学科的分数，每行显示某个学生学生。这里使用numpy的mean直接计算平均值

pri_mean = np.mean(score,axis=0)
pri_mean
#matrix([[76.66666667, 70.        , 55.        ]])

计算整个数据集的协方差矩阵

我们可以使用以下公式计算两个变量X和Y的协方差

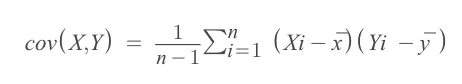cov_matrix 这里我们使用numpy.cov函数直接计算协方差矩阵排序分别为语文，数学，英语

cov_matrix = np.cov(score.T)
cov_matrix
#语文 数学 英语
#array([[146.66666667, 140.        ,  60.        ],
#       [140.        , 400.        ,  20.        ],
#     [ 60.        ,  20.        , 350.        ]])

#

这里要注意的几点是：沿对角线为各个学科分数在不同学生之间的分数差异，从score的差在矩阵中可以看出

数差异最大，语文分数差异最小，因此数学相对语文有更多的可变性，不同学生间数学成绩差异更大
数学和英语的协方差最小，因此数学成绩与英语成绩关系较小，通过数学对英语成绩预测就不可预测

计算特征向量和相应的特征值

特征向量是当对其进行线性变换时其方向保持不变的向量。因此，松地从上面的协方差矩阵中计算出特征值和特征向量。让a是正方形矩阵，ν是一个向量，而λ是一个参数使得Aν = λν,那么 λ为向量a的特征值，v为向量a的特征向量 A的特征值是以下特征方程的根

det(A-λI)=0

首先计算det（A-λI），I是一个单位矩阵：


# det(cov_matrix) - λ(I)

python的numpy的linalg.eig函数可以直接计算出特征向量和特征值

eigenvalue,eigenvector = np.linalg.eig(np.cov(score.T))
eigenvalue
#array([ 76.41469158, 477.07841359, 343.17356149])

eigenvector
#array([[-0.90804625,  0.4184661 ,  0.01838809],
#       [ 0.38228723,  0.84588381, -0.3719369 ],
#       [ 0.17119717,  0.33070638,  0.92807587]])

通过减少特征值对特征向量进行排序，并选择特征值最大的k个特征向量以形成d×k维矩阵W

我们的目标是减小特征空间的维数，即通过PCA将特征空间投影到较小的子空间，特征向量将在该子空间中形成该新特征子空间的轴。但是，特征向量仅定义新轴的方向，因为它们具有相同的单位长度1。因此，为了确定我们要为低维子空间删除的特征向量，我们必须查看特征向量的相应特征值。粗略地说，具有最低特征值的特征向量具有关于数据分布的最少信息，而这些正是我们要删除的特征向量。常用的方法是将特征向量进行排序，然后选择前k个特征向量。因此，在按降序对特征值进行排序后,选择特征向量最大的2项



idx = np.argsort(eigenvalue)[::-1]
idx #用于排序特征向量
#477.07841359,343.17356149,76.41469158


eigenvector = eigenvector[:,idx[:2]]
eigenvalue = eigenvalue[idx[:2]]

使用此d×k特征向量矩阵将样本转换到新的子空间上

获得并选择需要的k个特征向量后就可以使用点乘获得新的向量空间了，方法如下


new_matrix = np.dot(score, eigenvector)
new_matrix
#matrix([[114.87148787,  53.58478318],
#        [135.47858486,   1.58427232],
#        [132.75627721,  32.96203655],
#        [ 95.70337722,  34.4716232 ],
#        [ 96.58097443,  25.37474538],
#        [ 81.50800877,  10.53259702]])

总结

上面使用python的numpy包进行了手动的计算了pca并映射到了子空间，其实sklearn包已经把上述所有的过程直接进行了封装，这里直接把原始版的pca和sklearn的pca一起放在这里供需要进行pca计算的时候进行参考

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import decomposition
from sklearn import datasets
from sklearn.preprocessing import StandardScaler

score = np.matrix([[ 90,  60,  80],
        [ 90, 100,  40],
        [ 80,  90,  70],
        [ 60,  60,  60],
        [ 70,  60,  50],
        [ 70,  50,  30]])
#####raw numpy 版本
x_std = StandardScaler().fit_transform(score)
eigenvalue,eigenvector = np.linalg.eig(np.cov(x_std.T))
idx = np.argsort(eigenvalue)[::-1]

eigenvector = eigenvector[:,idx[:2]]
eigenvalue = eigenvalue[idx[:2]]
new_matrix = np.dot(x_std, eigenvector)
-new_matrix
#array([[-0.97429996, -1.49031278],
#       [-1.59492786,  1.54333152],
#       [-1.19990275, -0.32980079],
#       [ 1.29979933, -0.57553885],
#       [ 0.86561934,  0.00681518],
#       [ 1.60371189,  0.84550571]])

####sklearn版本
score = np.matrix([[ 90,  60,  80],
        [ 90, 100,  40],
        [ 80,  90,  70],
        [ 60,  60,  60],
        [ 70,  60,  50],
        [ 70,  50,  30]])
x_std = StandardScaler().fit_transform(score)
pca = decomposition.PCA(n_components=2)
pca.fit_transform(x_std)

#array([[-0.97429996, -1.49031278],
#       [-1.59492786,  1.54333152],
#       [-1.19990275, -0.32980079],
#       [ 1.29979933, -0.57553885],
#       [ 0.86561934,  0.00681518],
#       [ 1.60371189,  0.84550571]])

想要更加清楚pca原理，请先检查raw numpy版本，如果仅仅是获得pca后的结果，使用sklearn版本就好了。