一棵树在现实生活中有许多枝叶，事实上树的概念在机器学习也有广泛应用，涵盖了分类和回归。在决策分析中，决策树可用于直观地决策和作出决策。决策树，顾名思义，一个树状的决策模型。尽管数据挖掘与机器学习中常常用到，本文将集中说明决策树及python的实现。

如何将算法表示为树

为此，让我们考虑一个非常基本的示例，该示例采用泰坦尼克号数据集（该数据机可直接在sklearn获得）。该模型使用数据集中的3个特征，即性别，年龄和同胞（配偶或子女的数量） 维基的图。。。。 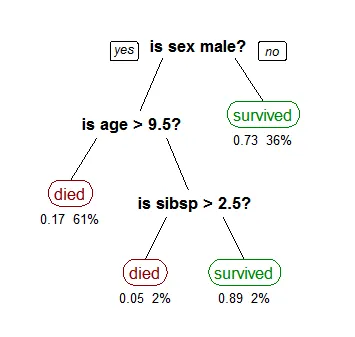titanic_decision 决策树是上下颠倒的，其根在顶部。在上图中，黑色粗体表示条件/ 内部节点，树将基于该条件分裂为分支/ 边缘。分支的末端不再分裂，是决策/ 叶子，在这种情况下，乘客是死亡还是幸存，分别用红色和绿色表示。 虽然，真实的数据集将具有更多的特征，而这只是展示了更大树中的一个分支，但是您不能忽略此算法的简单性。该功能重要性是显而易见的。这种方法通常称为从数据中学习决策树，而上方的树则称为分类树，因为目标是将乘客分类为是幸存还是死亡。回归树以相同的方式表示，只是它们预测的是像房屋价格这样的连续值。通常，决策树算法被称为CART或分类和回归树。 那么，后台实际发生了什么？种植一棵树涉及决定要选择的特征以及要使用的分割条件，以及何时停止。因为树通常会随心所欲地生长，因此您需要将其修剪减少决策树以使其节点适中防止过拟合的出现。 让我们从用于拆分的常用技术开始

分裂属性

首先需要将特征划分为2分类，像年龄，比如以9.5岁作为划分标准，一类为大于9.5岁，一类为小于9.5岁。 在此过程中，将考虑所有功能，并使用成本函数尝试并测试不同的分割点。选择成本最高（或成本最低）的拆分。考虑从泰坦尼克号数据集中学习的树的早期示例。在第一个分割或根中，将考虑所有属性/特征，并根据该分割将训练数据分为几组。我们选择了3个特征，因此将有3个候选分割。现在，我们将使用函数来计算每次拆分将使我们付出多少精度。选择成本最低的拆分，在我们的示例中为乘客性别。该算法本质上是递归的，因为可以使用相同的策略对形成的组进行细分。由于此过程，该算法也称为贪心算法，因为我们迫切希望降低成本。这使根节点成为最佳预测器/分类器。

分割成本

让我们仔细看看用于分类和回归的成本函数(cost function)。在这两种情况下，成本函数都试图找到大多数同质分支，或具有相似响应组的分支。这可以使我们更加确定测试数据输入将遵循特定路径。 回归：sum(y — prediction)²

可以说，我们正在预测房屋价格。现在，决策树将通过考虑训练数据中的每个功能来开始拆分。特定组的训练数据输入的响应平均值被视为该组的预测。上面的函数适用于所有数据点，并为所有候选分割计算成本。再次选择成本最低的拆分。 分类 : G = sum(pk * (1 — pk))

基尼系数可以通过拆分创建的组中的响应类别的混合程度来给出拆分的良好程度。在这里，pk是特定组中存在的相同类别输入的比例。当一个组包含来自同一类的所有输入时，便会出现完美的类纯度，在这种情况下，pk为1或0且G = 0，其中，在一个组中有50–50个类拆分的节点具有最差的纯度，因此对于二进制分类，它将具有pk = 0.5和G = 0.5

什么时候停止分裂

您可能会问何时停止种树？由于问题通常具有大量的特征，因此会导致大量分裂，从而产生一棵巨大的树。这样的树很复杂，极有可能导致过度拟合。因此，我们需要知道何时停止？一种方法是设置在每个叶子上使用的训练输入的最小数量。例如，该例子我们可以使用最少10位乘客来做出决定（去世或幸存），而忽略任何占用少于10位乘客的叶子。另一种方法是设置模型的最大深度。最大深度是指从根到叶的最长路径的长度。

修剪

通过修剪可以进一步提高树的性能。它涉及删除使用重要性低的功能的分支。这样，我们降低了树的复杂度，从而通过减少过拟合来提高树的预测能力。 修剪可以从根或叶开始。最简单的修剪方法从叶子开始，并删除该叶子中具有最流行类的每个节点，如果不降低准确性，则保留此更改。也称为减少错误修剪。可以使用更复杂的修剪方法，例如成本复杂度修剪，其中使用学习参数（alpha）权衡是否可以根据子树的大小删除节点。这也称为最弱链接修剪。

CART的优势

决策树的方法有ID3, C4.5, C5.0，cart，使用较多的是cart，而且sklearn中使用的也是cart的优化版本。因此这里只说明cart的优势

  • 易于理解，解释，可视化。
  • 决策树隐式执行变量筛选或特征选择。
  • 可以处理数值和分类数据。还可以处理多输出问题。
  • 决策树需要用户花费很少的精力进行数据准备。
  • 参数之间的非线性关系不会影响树的性能。

CART的缺点

  • 决策树学习可能会创建过于复杂的树，从而无法很好地概括数据。这称为过拟合。
  • 决策树可能不稳定，因为数据中的细微变化可能会导致生成完全不同的树。这称为方差，需要使用装袋和增强等方法降低 方差。
  • 贪婪算法不能保证返回全局最优决策树。这可以通过训练多棵树来缓解，其中可以随机替换特征和样本。
  • 如果某些特征占主导地位，决策树学习者会创建有偏见的树。因此，建议在与决策树拟合之前平衡数据集。

python 实现

介绍完决策树后，我们这里将演示sklearn的决策树的实现。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix

text = requests.get("https://www.bobobk.com/wp-content/uploads/2020/01/train.csv").text
with open("train.csv",'w') as fw:
    fw.write(text)
titanic = pd.read_csv("train.csv")


titanic["Age"] = titanic["Age"].fillna(titanic["Age"].median())
titanic["Embarked"] = titanic["Embarked"].fillna("S")
candidate_train_predictors = titanic.drop(['PassengerId','Survived','Name','Ticket','Cabin'], axis=1)
categorical_cols = [cname for cname in candidate_train_predictors.columns if 
                                candidate_train_predictors[cname].nunique() < 10 and
                                candidate_train_predictors[cname].dtype == "object"]
numeric_cols = [cname for cname in candidate_train_predictors.columns if 
                                candidate_train_predictors[cname].dtype in ['int64', 'float64']]
my_cols = categorical_cols + numeric_cols
train_predictors = candidate_train_predictors[my_cols]
dummy_encoded_train_predictors = pd.get_dummies(train_predictors)
######
y_target = titanic["Survived"].values
x_features_one = dummy_encoded_train_predictors.values
x_train, x_validation, y_train, y_validation = train_test_split(x_features_one,y_target,test_size=.25,random_state=1)
print(x_features_one)

#####
tree_one = tree.DecisionTreeClassifier()
tree_one = tree_one.fit(x_features_one, y_target)
tree_one_accuracy = round(tree_one.score(x_features_one, y_target), 4)
print("准确度: %0.4f" % (tree_one_accuracy))

#准确度: 0.9798